Savage Solder: Measuring Localization Accuracy Part 3
In Part 1 and Part 2, I described why we’re trying to measure localization accuracy, and the properties of a GPS receiver that allows us to do so. In this post, I’ll describe the technique we used to measure accuracy of our solution purely from recorded data, without needing to go back out to the field every time a change was made.
Our solution
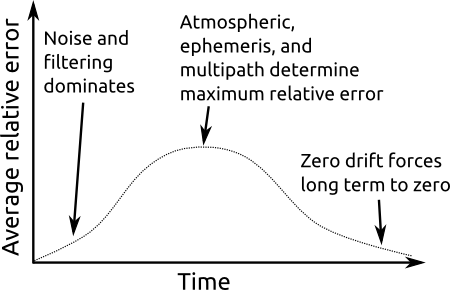
The technique we used to measure localization accuracy is somewhat similar to the Allan Variance plots used in part 2. Here, we take a large corpus of pre-recorded sensor data from the vehicle and re-run it through the localization solution. The trick is that for a given time window, the GPS updates are witheld from the filter, then at the end of the window, the difference between the estimated position and the measured GPS position is recorded. The cycle then starts anew at the current time, with the estimate being reset to the best possible one, and GPS denied until the next window end. Each sampled error is one data point showing how far off the localization solution can be after that much time with no GPS.
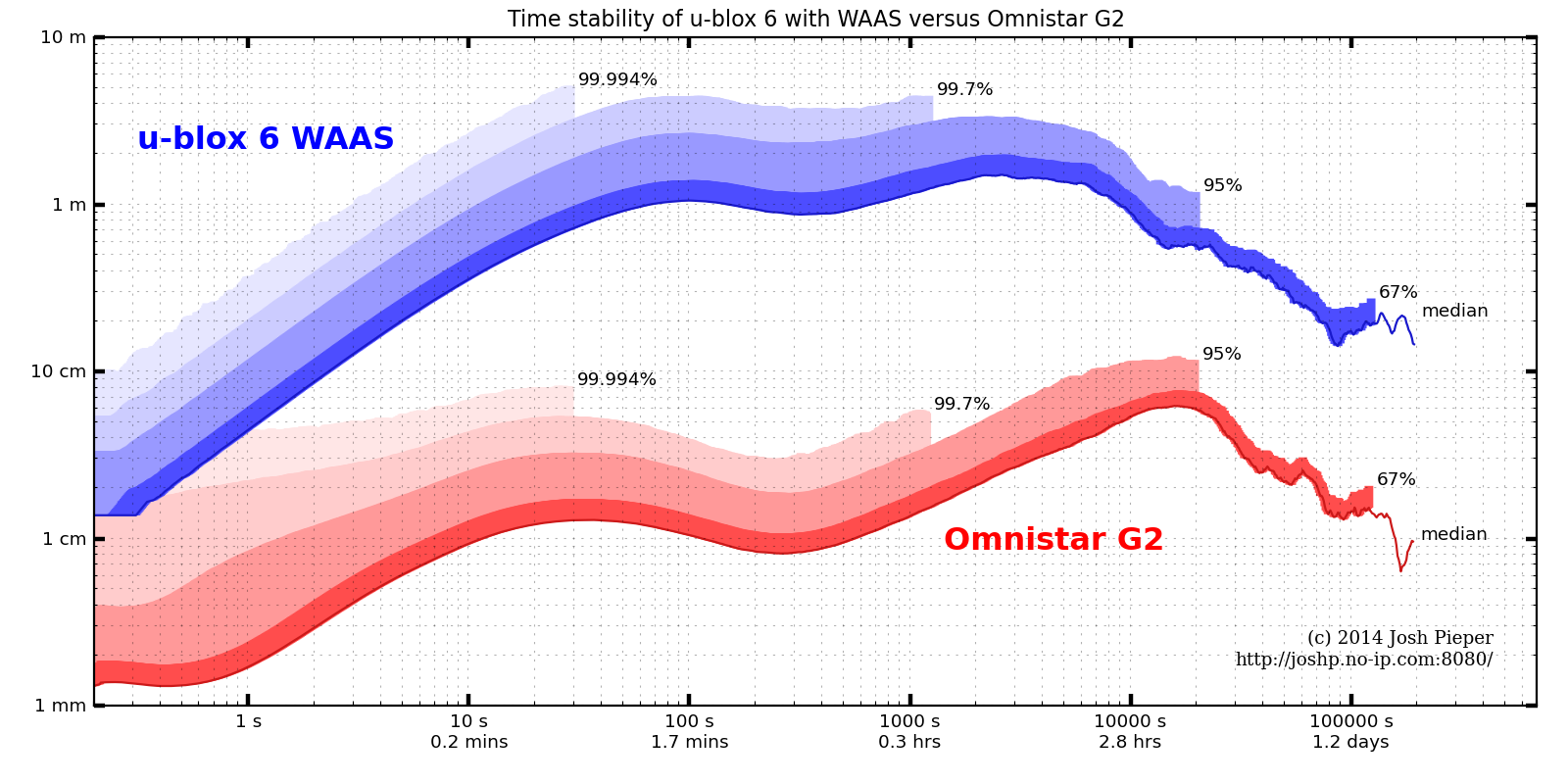
We expect this to be effective because, as the plots in part 2 showed, over short time windows, the average drift in the GPS is actually pretty small. For instance, the u-blox 6 on savage solder, within a 5s time window, will have drifted only about 0.6m with 95% confidence.
Once the results have been collated for a given time window, say 1s, we repeat the entire process for 2s, then 3s, etc. The curves this produces show how rapidly the position error in localization grows with time. The lower the value is at longer time intervals, that means the vehicle is more robust to GPS outages or drifts.
Results on Savage Solder’s 2013 AVC software
A plot of our 2013 AVC localization solution’s accuracy is shown below. It was measured over about 30 minutes of autonomous driving, mostly recorded in the weeks leading up to the 2013 AVC. I have superimposed on it the 68% and 95% confidence in the u-blox drift for reference. If the localization solution were perfect, we would expect the measured errors to approximately line up with the GPS drift over the same time interval.
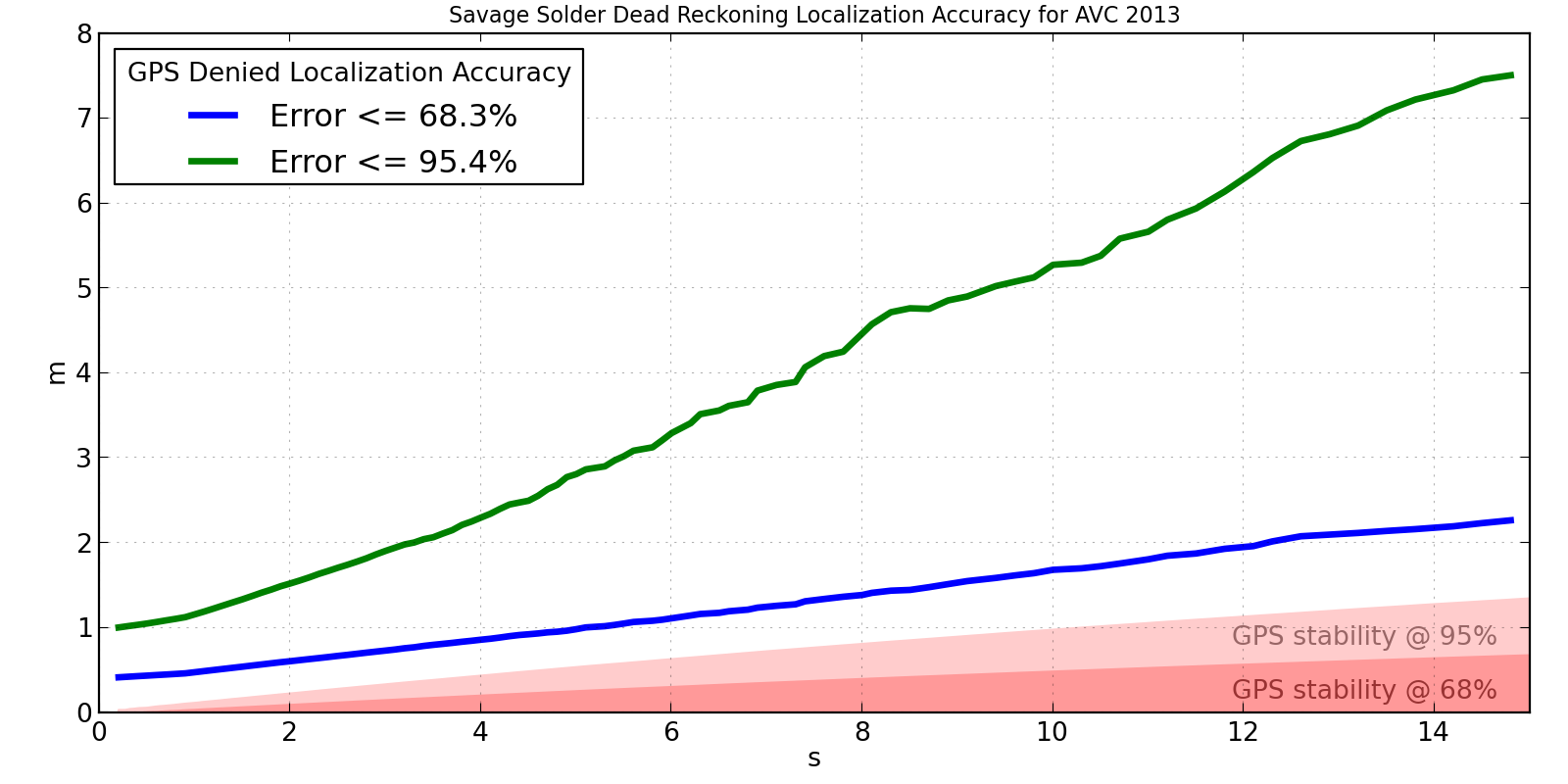
Savage Solder AVC 2013 Localization Accuracy
This shows that the accuracy isn’t terrible, but isn’t particularly great either. After 15 seconds, it is off by less than 2m two thirds of the time. However, in order to capture the best 95% of results, we have to look all the way out to 7.5m, which clearly isn’t too usable. For a course like the Sparkfun AVC one, you can roughly say that errors larger than 2 or 3 meters will result in a collision with something. This implies that Savage Solder can run for about 3 to 5 seconds with no GPS and be not terrible.
We have a couple of theories for where the largest sources of error are in the system as shown in the above plot:
- Initial heading error: For all of these data sets, the car has only a very rough knowledge of its heading when starting out and all information about the heading comes from GPS. Even a small initial heading error will result in large position errors early in each run.
- Total state filter: As described before the localization solution used during 2013 was a total state Kalman filter. I expect that switching to an error state can improve the performance.
- Improved inertial sensors: This can’t strictly be tested after the fact, but there now exist easily obtainable higher quality gyroscopes and accelerometers than the Pololu MiniIMU v2 we used in 2013.
Recap of measuring localization accuracy
Looking back at part 1, this technique measures up pretty well. It:
- requires only data recorded on the robot, it
- provides hard numeric results (within the limits of the GPS’s short term drift), and it
- requires no additional sensors
You can tweak the localization algorithms in software as many times as necessary, each time accurately assessing the results, and never once need to go out and actually drive the robot around.