Savage Solder: Measuring Localization Accuracy Part 2
In Part 1, I discussed how measuring the accuracy of a localization solution in a mobile robot is challenging, and some properties an ideal solution would have. This time, I’ll describe some of the properties of the GPS receiver Savage Solder uses, to motivate our mechanism for using it to measure localization accuracy.
Principles
The basic idea behind our approach is that the GPS mounted on Savage Solder, while relatively inaccurate in general, rarely has a very large error. And even when the error is large, it is usually only for a short window of time. Over time, these periods where the GPS has a lot of error come and go semi-randomly, which means that with enough data, they will tend to average out. To see how this works in a little more detail, let’s talk about the major sources of error that a GPS receiver can have.

NASA rendering of GPS satellite
Geometry and clock error: At any given instant, only a subset of the GPS satellites are visible to a receiver, and those that are visible will have a configuration which introduces a source of error due to the process of triangulation. For instance, if all the visible satellites are in the same part of the sky, measuring ranges to the satellites will not tell you much about your absolute position. Secondly, each satellite may have differing errors in their onboard clocks, each of which translates directly in range measurement errors. Both of these error sources change relatively slowly with time.
Ephemeris and atmospheric effects: To estimate its location, a receiver must have precise knowledge of each satellite’s orbit, or ephemeris. While this orbit is known relatively precisely, every centimeter of error directly corresponds to positioning error on the ground. Ephemeris errors typically change slowly over time, as space weather isn’t as drastic as Boston weather. Atmospheric effects have similar properties when visible from the receiver, the ionosphere is the primary factor, as it causes delays in the signals propagating from the satellites to each receiver. Its effects also change relatively slowly with time.
Multipath and obstructions: When the line of sight to a receiver is blocked by a tree, building, person, vehicle, or the horizon, that can cause the signal to weaken enough to mis-register. The receiver can also pick up reflections of the actual satellite signal from any of the above. These reflected signals are called “multi-path”, and they cause the receiver to measure the additional length in the reflected path, instead of the true shortest path. As new satellites become available or are hidden, they can join or fall out of the solution. These errors can change rapidly for ground vehicles, where the line of sight to satellites can rapidly become clear or obstructed as it moves around.
Noise: Each measurement has some amount of random noise associated with it. Consumer receivers typically only measure the code phase, and not the carrier phase, so this measurement noise can be on the order of a meter or so for each satellite. It has mostly high frequency components.
Filtering: In order for the output to look more “reasonable”, most low-cost consumer receivers implement some sort of state estimation filtering before emitting any outputs. This smooths out noise components, and also smooths out rapid changes in multi-path or which satellites are used in the solution. As a result, the final position can often seem smooth, but as a result has more absolute error at any given instant.
Windowed error measurement
To get an idea of the magnitude of each of these error types, we used a technique similar to Allan Variance to see the magnitude of error from the GPS solution in differing time domains. A long recording of reported GPS positions is made while the receiver is stationary. Then, it is divided up first into say consecutive 0.2s windows. Within each window the position is averaged, after which the change between consecutive windows is measured. These deltas represent how much the receiver’s absolute offset has drifted in that time period. For the 0.2s size, you can then see how much the offset changes on average, or how much it changes 95% of the time.
Once you’ve done that for the first window size, you increase the window size, say to 0.3s and repeat the whole process. You keep increasing the window size until you can only fit a few bins into the recorded trace.
What we expect to see is something like the following:
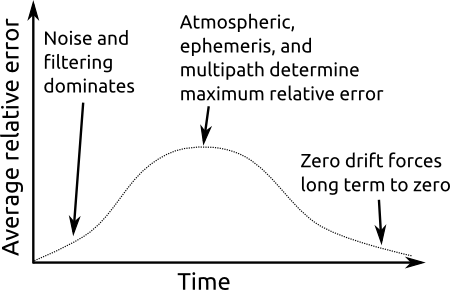
Typical GPS relative error plot
At very high frequencies (short time intervals), the filtering on the receiver renders the errors small. This means that on average, the position doesn’t change much over short intervals. Then, as the time interval gets up into the 5 to 60 minutes range, the error rapidly increases as we see the effects of atmospheric, ephemeris, and multipath errors become realized. Eventually, the error will peak, at a time interval which depends upon what the worst error contributor is. Finally, as the time grows to infinity, we would expect to see the error drop off, as averaging over such large time intervals tends to reveal the zero-drift property of GPS.
We ran this experiment on the u-blox 6 GPS used on Savage Solder and a high quality dual frequency receiver outfitted with Omnistar G2 as a reference. The u-blox was very crudely weatherized for long term outdoor recording with a disposable tupperware container. A recording at full data rate for each GPS was made over about 16 days of operation. Each GPS’s plot shows the median error and the maximum expected error for differing probabilities, which equate to about 1, 2, and 3 sigma on a normal distribution. (The non-weatherized u-blox was tested over a shorter duration and appeared to produce equivalent results.)
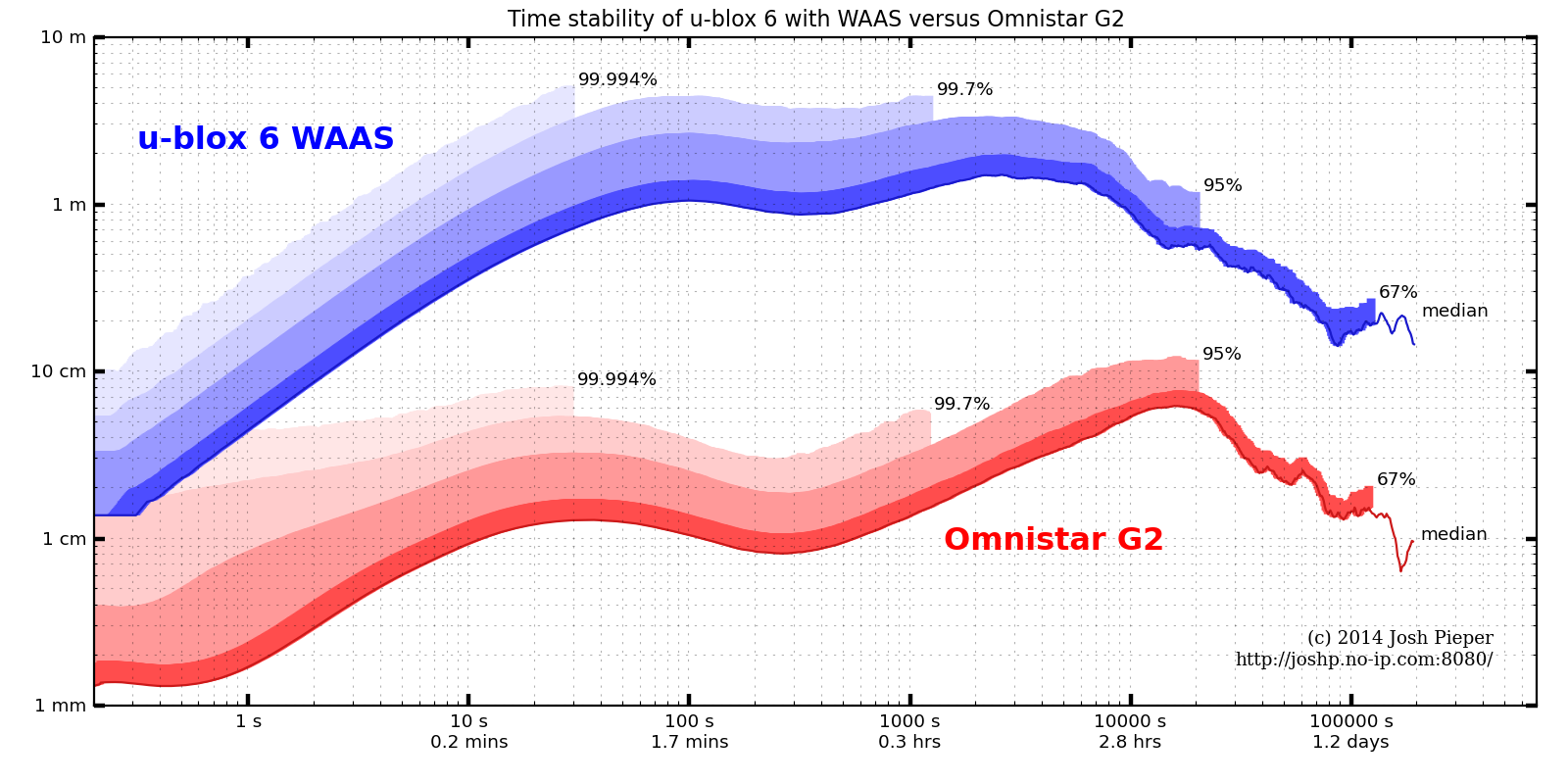
Time stability of u-blox 6 with WAAS versus Omnistar G2.
Analysis
The data was taken while stationary on a rooftop with clear 360 degree view of the sky, and thus has best case visibility. Results on an AVC style course will be worse, since multi-path and obstructions will be constantly changing. Despite that, we can get some lower bounds on how good the system could possibly be from these results.
For instance, for a time commensurate with a Sparkfun AVC course run (about 45 seconds for a fast vehicle), the u-blox can be expected to drift around 2.2 meters with 95% confidence. The maximum drift over any interval with 95% confidence is around 3.3m, which implies that it is dicey to survey the course in ahead of time and expect the measurements to be useful. Also, the time required before averaging measurements actually starts to improve stability is pretty long. For the u-blox, it is around 1 hour, and even after looking at an entire day, the stability only gets down to around 24cm.
It is important to note that while the u-blox reports a GPS accuracy metric at any given time, it is usually extremely optimistic. For most of the above trace, the accuracy was reported as about 0.5m with a 1 sigma probability, when the measured absolute 1 sigma accuracy was clearly around 2m or more.
As a reference, the Omnistar G2 trace shows that yes, its performance is about 2 orders of magnitude better than the low-cost u-blox receiver. In these near-ideal conditions, it has a 95% confident maximum error of around 12cm, which means that it could be viable for hitting the hoop and ramp. However, as this is in ideal conditions, shading and multipath from the course, spectators, and other vehicles will certainly make actual results even worse.
Using this
In the next post, I’ll show how we used this knowledge of our GPS receiver’s error properties to measure the quality of our localization solution over short to medium time intervals.

