Savage Solder: Tracking Cones
Last time I covered the techniques we use on Savage Solder to pick out orange traffic cones from webcam images in the “Cone Detector”. This time, I’ll look at the next stage in that pipeline, turning the range and bearing reported by the cone tracker into Cartesian coordinate estimates of where any given cone is.
Cone Tracker Overview
As mentioned last time, our “Cone Tracker” takes as input the range and bearing, (along with their uncertainties), from the cone detector. It also receives the current navigation state of the car. This includes things like the current estimate of geodetic position (latitude and longitude), current map position, (UTM easting and northing), and an unreferenced local coordinate system (x, y). For each of these, it reports the vehicle’s speed and heading.
I won’t go into the details of each of these coordinate systems here, but since the cone tracker actually only uses the local one, I can discuss it a bit. The local coordinate system on Savage Solder starts out at x,y=(0m,0m) with a heading of 0 degrees at the beginning of every run. As time progresses, the heading and position are updated primarily based on our onboard dead reckoning sensors. The local coordinate system is smooth, and never jumps for GPS updates. As a consequence, it isn’t really useful to compare positions in it from more than a minute or two apart, nor is it useful to do GPS based navigation. Fortunately, for cone tracking, from the time to when we see the cone to when we touch it is usually only a couple of seconds total over which time the local solution is very accurate.
Now, let’s cover some broad details of the implementation. The guts of our cone tracker consists of a bank of identical Kalman Filters. Each Kalman filter estimates the position of one particular cone and the error in that estimate. This lets the car keep around several possible cones that could be in sight at one time while still distinguishing them. By storing the cones in a local coordinate system, it allows for easy driving towards, or alongside, the cone and accurate speed control leading up to it. The position uncertainty could be used to control behavior, but we don’t bother in our current implementation.
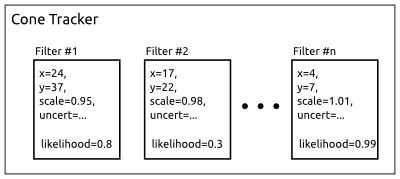
Cone Tracker Internals
New and Old Cones
Additionally, the tracker has to handle seeing new cones for the first time, and discarding cones that maybe were false detections in the cone detector. It does this by assigning each cone a “likelihood”, which is just a probability that the cone is a true detection. When data arrives that match the cone well, its likelihood is increased. When the available data doesn’t match the cone very well, or no cone is observed at all when one is expected, the likelihood is decreased.
If a range and bearing arrive which corresponds to no known cones, a new one is created with a relatively low likelihood. Then once it has reached a certain threshold, it is reported to the outside world as a valid target. Conversely, when an existing cone’s likelihood reaches a level which is too low, it is removed entirely on the thesis that it was actually a false detection to begin with.
More specifically, the likelihood update is handled using Bayes theorem. We have an empirically derived table showing, for our detector, the odds that a cone will be detected or a false one will be seen at various ranges. These are used to fill in the various probabilities in the equations.
Incorporating New Measurements
A “measurement” in this problem is simply the range and bearing that the cone detector reports. To incorporate a new measurement, the tracker looks through all the cones currently in its filter bank. For each, it computes a measure of the likelihood that the given cone could produce the current measurement. This is done using what’s called the Mahalanobis distance. The Mahalanobis distance is just a measure of how far away you are from an uncertain target in a multi-dimensional space.
If the best matching cone has a Mahalanobis distance small enough to count as valid, then the standard Kalman filter update equation is applied to that cone. If no cones match, then we create a new one as described above.
Scale Factor
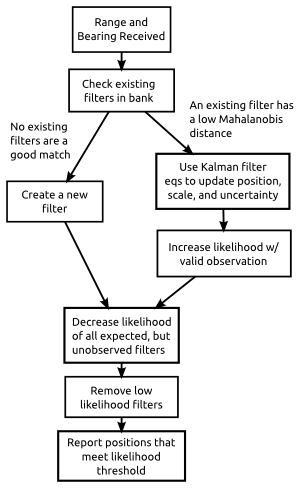
Cone Tracker Flowchart
One final detail, is that in addition to estimating the position of each cone, the tracker also estimates its “scale” as seen by the cone detector. The image based detector we use has the property that the range values are likely to have a fixed scale error for a number of reasons. One, the cones could actually be bigger or smaller than the regulation sized ones. Second, lighting conditions can sometimes cause a fraction of the cone to be not detected, which will result in the cone being seen as smaller than it actually is.
Since the range values are not correct, the position will be similarly off. This error isn’t as bad as it seems, since we (and most every RoboMagellan entrant), approach the cone in a straight line. Thus the position errors will always be directly towards or away from the robot, and as long as you keep moving, you’ll hit it eventually.
Savage Solder has two reasons to care. First, is that we decelerate from a high speed to an appropriate “bumping” speed with just a half meter to spare. Thus, if the cone is estimated as too close, we run the risk of colliding with it at an unsafe speed and damaging our front end. Secondly, we have a mode where the car can just “clip” the cone by driving alongside it and tapping it with a protruding stick. This allows us to avoid stopping entirely when the geometry allows it. However, if the position estimate is incorrect here, we might miss the cone entirely.
Final Process
To summarize, the cone tracker handles each new range and bearing with the following steps:
- A cone detection results in a new range, bearing, and uncertainty measurement.
- Existing cones in the Kalman filter bank are checked to see what the likelihood is each could have produced this measurement.
- If one was likely enough, then:
- The position and scale factor are updated using the Kalman filter equations.
- The likelihood estimate is updated according to our current false positive and false negative estimates.
- If none was likely enough, then a new cone is created with a position fixed at the exact position implied by the local navigation solution and the range and bearing.
- Any cones which we had expected to see but didn’t have their likelihood decreased.
- Any cones which have too low of a likelihood are removed.
- Finally, all the cones which are close to the vehicle, and have a high enough likelihood are reported to the high level logic.
Caveats and Next Steps
One of the challenges with this approach is that there are a lot of constants to tune. I’ll cover the details in a later post, but for most of them we tried to find some way to empirically measure reasonable values for our application. Another problem was debugging. printf doesn’t cut it when you have this much geometry. For that, we created a number of custom debugging and visualization tools which help show what is going on in the system, some of which I’ll cover later too.